OS PROGRAMS

LFU

Producer Consumer Program

Program

Programs

Allocation Methods

Shell and C Programs

Shell

C Program

Shell Scripting

Programs

SCHEDULING ALGORITHMS

LINK

OS PROGRAMS

Link

UNIX NOTES

UNIX commands

shortcuts

GRAY LEVEL TRANSFORMATION

Image enhancement is a very basic image processing task that defines us to have a better subjective judgement over the images. And Image Enhancement in spatial domain (that is, performing operations directly on pixel values) is the very simplistic approach. Enhanced images provide better contrast of the details that images contain. Image enhancement is applied in every field where images are ought to be understood and analysed. For example, Medical Image Analysis, Analysis of images from satellites, etc. Here I discuss some preliminary image enhancement techniques that are applicable for grey scale images.

Image enhancement simply means, transforming an image f into image g using T. Where T is the transformation. The values of pixels in images f and g are denoted by rand s, respectively. As said, the pixel values r and s are related by the expression,

s = T(r)

where T is a transformation that maps a pixel value r into a pixel value s. The results of this transformation are mapped into the grey sclale range as we are dealing here only with grey scale digital images. So, the results are mapped back into the range [0, L-1], where L=2^k, k being the number of bits in the image being considered. So, for instance, for an 8-bit image the range of pixel values will be [0, 255].

There are three basic types of functions (transformations) that are used frequently in image enhancement. They are,

• Linear,
• Logarithmic,
• Power-Law.

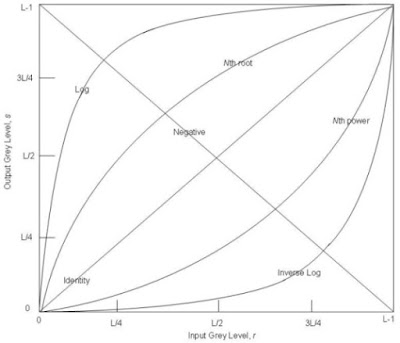
The transformation map plot shown below depicts various curves that fall into the above three types of enhancement techniques.

The Identity and Negative curves fall under the category of linear functions. Indentity curve simply indicates that input image is equal to the output image. The Log and Inverse-Log curves fall under the category of Logarithmic functions and nth root and nth power transformations fall under the category of Power-Law functions.

Image Negation

The negative of an image with grey levels in the range [0, L-1] is obtained by the negative transformation shown in figure above, which is given by the expression,

s = L - 1 - r

This expression results in reversing of the grey level intensities of the image thereby producing a negative like image. The ouput of this function can be directly mapped into the grey scale look-up table consisting values from 0 to L-1.

Log Transformations

The log transformation curve shown in fig. A, is given by the expression,

s = c log(1 + r)

where c is a constant and it is assumed that r≥0. The shape of the log curve in fig. A tells that this transformation maps a narrow range of low-level grey scale intensities into a wider range of output values. And similarly maps the wide range of high-level grey scale intensities into a narrow range of high level output values. The opposite of this applies for inverse-log transform. This transform is used to expand values of dark pixels and compress values of bright pixels.

Power-Law Transformations

The nth power and nth root curves shown in fig. A can be given by the expression,

s = cr^γ

This transformation function is also called as gamma correction. For various values of γ different levels of enhancements can be obtained. This technique is quite commonly called as Gamma Correction. If you notice, different display monitors display images at different intensities and clarity. That means, every monitor has built-in gamma correction in it with certain gamma ranges and so a good monitor automatically corrects all the images displayed on it for the best contrast to give user the best experience.

The difference between the log-transformation function and the power-law functions is that using the power-law function a family of possible transformation curves can be obtained just by varying the λ.

These are the three basic image enhancement functions for grey scale images that can be applied easily for any type of image for better contrast and highlighting. Using the image negation formula given above, it is not necessary for the results to be mapped into the grey scale range [0, L-1]. Output of L-1-r automatically falls in the range of [0, L-1]. But for the Log and Power-Law transformations resulting values are often quite distintive, depending upon control parameters like λ and logarithmic scales. So the results of these values should be mapped back to the grey scale range to get a meaningful output image. For example, Log function s = c log(1 + r) results in 0 and 2.41 for r varying between 0 and 255, keeping c=1. So, the range [0, 2.41] should be mapped to [0, L-1] for getting a meaningful image.

Reference:
Gonzalez C. R., Woods E. R., Digital Image Processing, 2nd Ed.,

TYPES OF IMAGES

Images can be classified as follows:

• Monochrome image (Binary images).
• Grey scale images.
• Color (24-bit) images.
• Half-toned images. -

1. Monochrome Image

In this, each pixel is stored as a single bit (0 or 1.) Here, 0 represents black while 1 represents while. It is a black and white image in the strictest sense. These images are also called bit mapped images; we have only black and white pixels and no other shades of grey.

2. Grey scale Image

Here each pixel is usually stored as a byte (8-bits). Due to this, each pixel can have values ranging from 0(black) to 255(white). Grey scale images, as the name suggests have black, white and various shades of grey present in the image.

3.Color Image (24-bit)

Color images are based on the fact that a variety of colors can be generated by mixing the three primary colors viz, Red, Green and Blue, in proper proportions. In color images, each pixel is composed of RGB values each of these colors require 8-bits (one byte) for it’s represented by 24-bits [R (8-bits,), G (8-bits), B (8-bits)].

A 24-bit color image supports 16, 777,216 different combinations of colors. Color images can be easily converted to grey scale images using the equation

X = 0.30R + 0.59G + 0.11B

An easier formula that could achieve similar results is

Half Toning

It is obvious that a grey scale image definitely looks than the monochrome image as it utilizes more grey levels. But there is a problem in hand. Most of the printers, that we use (inkjet, lasers, dot matrix) are all bi-level devices. i.e., they have only a black cartridge and can only produce two levels (black on a white back-ground). In fact, most of the printing jobs are done using bi-level devices.

SAMPLING AND QUANTIZATION

An image may be continuous w.r.t x and y co-ordinate and also in amplitude. To convert it to digital form, we have to sample the function in both co-ordinate and amplitude.

Sampling :

• The process of digitizing the co-ordinate values is called Sampling.
• A continuous image f(x, y) is normally approximated by equally spaced samples arranged in the form of a NxM array where each elements of the array is a discrete quantity.

• The sampling rate of digitizer determines the spatial resolution of digitized image.
• Finer the sampling (i.e. increasing M and N), the better the approximation of continuous image function f(x, y).

Quantization :

• The process of digitizing the amplitude values is called Quantization.
• Magnitude of sampled image is expressed as the digital values in Image processing.
• No of quantization levels should be high enough for human perception of the fine details in the image.
• Most digital IP devices uses quantization into k equal intervals.
• If b-bits are used,

No. of quantization levels = k = 2b$2^b$

• 8 bits/pixels are used commonly.

COMPONENTS OF DIGITAL IMAGE PROCESSING

In sensing, two elements are required to acquire digital images.

The first is physical device that is sensitive to the energy radiated by the object we wish to image.

The second called a digitizer, is a device for converting the output of the physical sensing device into digital form.

Specialized image processing hardware usually consists of the digitizer plus hardware that performs other primitive operations such as arithmetic and logical operations (ALU). Eg. Noise reduction. This type of hardware sometimes is called a front end subsystem.

The computer is an image processing system is a general purpose to supercomputer Software which include image processing specialized modules that performs specific tasks Mass storage capability is a must in image processing applications.

Image displays in use today are mainly color TV monitors.

Hardcopy devices for recording images include laser printers, film cameras, inkjet units and CD-ROM.